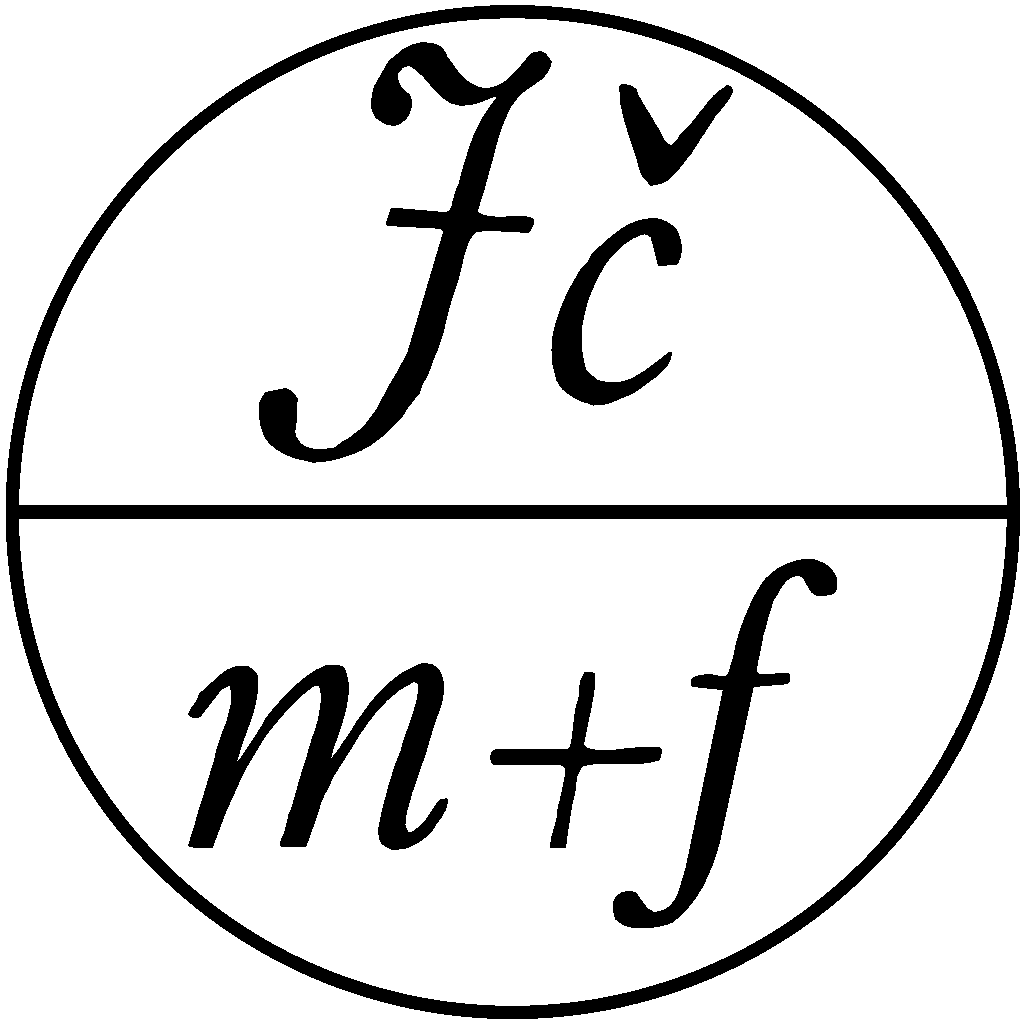Combinatorial proofs of identities with Fibonacci numbers
Abstract
The article presents four selected identities, which describe properties of the Fibonacci numbers. The task is to prove the validity of these identities in a way that is less common but more elegant, namely by means of a combinatorial argument. For that purpose the relationship between Fibonacci numbers and the number of all possible tiles of a rectangle 1×n with 1×1 and 1×2 polyominoes is used.Downloads
Published
How to Cite
Issue
Section
License
Autoři, kteří publikují v tomto časopise, souhlasí s následujícími body:
- Autoři si ponechávají copyright a garantují časopisu právo prvního publikování, přitom je práce zároveň licencována pod Creative Commons Attribution licencí, která umožňuje ostatním sdílet tuto práci s tím, že přiznají jejího autora a první publikování v tomto časopisu.
- Autoři mohou vstupovat do dalších samostatných smluvních dohod pro neexkluzivní šíření práce ve verzi, ve které byla publikována v časopise (například publikovat ji v knize), avšak s tím, že přiznají její první publikování v tomto časopisu.

Obsah časopisu podléhá licenci Creative Commons Uveďte autora 3.0 Česko